Многочлены Лежандра

Многочлен Лежа́ндра — многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического. Образует ортогональную систему многочленов на отрезке [math]\displaystyle{ [-1,\;1] }[/math] в пространстве [math]\displaystyle{ L^2 }[/math]. Многочлены Лежандра могут быть получены из многочленов [math]\displaystyle{ \{1,\;x,\;x^2,\;x^3,\;\ldots\} }[/math] ортогонализацией Грама ― Шмидта.

Названы по имени французского математика Адриен Мари Лежандра.

Определение

Полиномы Лежандра и присоединённые функции Лежандра первого и второго рода

Рассмотрим дифференциальное уравнение вида

[math]\displaystyle{ (1-z^2) \frac{\mathrm d^2u}{\mathrm dz^2}-2z\frac{\mathrm du}{\mathrm dz} + n(n+1)u = 0, }[/math]

(1)

где [math]\displaystyle{ z }[/math] — комплексная переменная. Решения этого уравнения при целых [math]\displaystyle{ n }[/math] имеют вид многочленов, называемых многочленами Лежандра. Полином Лежандра степени [math]\displaystyle{ n }[/math] можно представить через формулу Родрига в виде

[math]\displaystyle{ P_n(z)=\frac{1}{2^n n!}\frac{d^n}{dz^n}(z^2-1)^n. }[/math]

Часто вместо [math]\displaystyle{ z }[/math] записывают косинус полярного угла:

[math]\displaystyle{ P_n(\cos\theta)=\frac{1}{2^n n!}\frac{d^n}{d(\cos\theta)^n}(\cos^2\theta-1)^n. }[/math]

Уравнение (1) можно получить из частного случая гипергеометрического уравнения, называемого уравнением Лежандра

[math]\displaystyle{ (1-z^2) \frac{\mathrm d^2u}{\mathrm dz^2}-2z\frac{\mathrm du}{\mathrm dz} + \left[ \nu(\nu+1) - \frac{\mu^2}{1-z^2}\right]u = 0, }[/math]

(2)

где [math]\displaystyle{ \mu }[/math], [math]\displaystyle{ \nu }[/math] — произвольные комплексные постоянные. Интерес представляют его решения, являющиеся однозначными и регулярными при [math]\displaystyle{ |z| \lt 1 }[/math] (в частности, при действительных [math]\displaystyle{ z }[/math]) или когда действительная часть числа [math]\displaystyle{ z }[/math] больше единицы. Его решения называют присоединёнными функциями Лежандра или сферическими функциями (гармониками). Подстановка вида [math]\displaystyle{ w = (z^2-1)^{\mu/2} }[/math] в (2) даёт уравнение Гаусса, решение которого в области [math]\displaystyle{ |1 - z| \lt 2 }[/math] принимает вид

[math]\displaystyle{ w = P_\nu^\mu(z)=\frac{1}{\Gamma(1-\mu)} \left( \frac{z+1}{z-1} \right)^{\mu/2} F\left(-\nu,\;\nu+1;\; 1-\mu;\; \frac{1}{2} - \frac{z}{2} \right), }[/math]

где [math]\displaystyle{ F }[/math] — гипергеометрическая функция. Подстановка [math]\displaystyle{ w = z^2 }[/math] в (2) приводит к решению вида

[math]\displaystyle{ w = Q_\nu^\mu(z)= e^{\mu i \pi} 2^{-\nu-1}\sqrt{\pi} \frac{\Gamma(\nu+\mu+1)}{\Gamma(\nu+3/2)} z^{-\nu-\mu-1}(z^2-1)^{\mu/2} F\left(\frac{\nu}{2}+\frac{\mu}{2}+1,\;\frac{\nu}{2}+\frac{\mu}{2}+\frac{1}{2};\; \nu+\frac{3}{2};\; z^{-2} \right), }[/math]

определённым на [math]\displaystyle{ |z|\gt 1 }[/math]. Функции [math]\displaystyle{ P_\nu^\mu(z) }[/math] и [math]\displaystyle{ Q_\nu^\mu(z) }[/math] называют функциями Лежандра первого и второго рода.

Справедливы соотношения

[math]\displaystyle{ P_\nu^\mu(z) = P_{-\nu-1}^\mu(z) }[/math]

и

[math]\displaystyle{ Q_\nu^\mu(z) \sin\pi(\nu+\mu) - Q_{-\nu-1}^\mu(z) \sin\pi(\nu-\mu) = \pi e^{i\mu\pi}\cos(\nu\pi)P_\nu^\mu(z). }[/math]

Выражение через суммы

Многочлены Лежандра также определяются по следующей формуле:

[math]\displaystyle{ P_n(x) = \frac{1}{2^n} \sum_{k=0}^{E(n/2)} (-1)^k \binom{n}{k} \binom{2n-2k}{n} x^{n-2k}. }[/math]

Рекуррентная формула

Они также могут быть вычислены по рекуррентной формуле (при [math]\displaystyle{ n \geqslant 1 }[/math]):

[math]\displaystyle{ P_{n+1}(x) = \frac{2n + 1}{n + 1} x P_n(x) - \frac{n}{n + 1} P_{n-1}(x), }[/math]

(3)

причём первые две функции имеют вид

[math]\displaystyle{ P_0(x) = 1, }[/math]

[math]\displaystyle{ P_1(x) = x. }[/math]

Производная полинома Лежандра

Вычисляется по формуле

[math]\displaystyle{ P'_{n}(x) = \frac{n}{1 - x^2} [P_{n-1}(x) - x P_n(x)]. }[/math]

(4)

Корни полинома Лежандра

Вычисляются итеративно по методу Ньютона:

[math]\displaystyle{ x_i^{(k+1)} = x_i^{(k)} - \frac{P_{n}(x_i^{(k)})}{P'_{n}(x_i^{(k)})}, }[/math]

причём начальное приближение для [math]\displaystyle{ i }[/math]-го корня ([math]\displaystyle{ i = 1,\;2,\;\ldots,\;n }[/math]) берётся по формуле

[math]\displaystyle{ x_i^{(0)} = \cos\frac{\pi (4i - 1)}{4n + 2}. }[/math]

Значение полинома можно вычислять, используя рекуррентную формулу для конкретного значения x. Производную также можно вычислять для конкретного значения x, используя формулу для производной.

Формулы с разложениями

Многочлены Лежандра также определяются следующими разложениями:

[math]\displaystyle{ (1 - 2tx + t^2)^{-\frac{1}{2}} = \sum_{n=0}^\infty P_n(x)t^n }[/math]   для   [math]\displaystyle{ |t| \lt \min\left|x \pm \sqrt{x^2 - 1}\right|, }[/math]

[math]\displaystyle{ (1 - 2tx + t^2)^{-\frac{1}{2}} = \sum_{n=0}^\infty P_n(x) \frac{1}{t^{n+1}} }[/math]   для   [math]\displaystyle{ |t| \gt \max\left|x \pm \sqrt{x^2 - 1}\right|. }[/math]

Следовательно,

[math]\displaystyle{ P_n(x) = \frac{(2n)!}{2^n(n!)^2} \left[x^n - \frac{n(n - 1)}{2(2n - 1)} x^{n-2} + \frac{n(n - 1)(n - 2)(n - 3)}{2 \cdot 4(2n - 1)(2n - 3)} x^{n-4} - \ldots\right]. }[/math]

Присоединённые многочлены Лежандра

Присоединённые многочлены Лежандра определяются по формуле

[math]\displaystyle{ P^m_n(x) = (1 - x^2)^{m/2} \frac{d^m}{dx^m} P_n(x), }[/math]

которую также можно представить в виде

[math]\displaystyle{ P^m_n(\cos\theta) = \sin^m\theta \frac{d^m}{d(\cos\theta)^m} P_n(\cos\theta). }[/math]

При [math]\displaystyle{ m = 0 }[/math] функция [math]\displaystyle{ P^m_n }[/math] совпадает с [math]\displaystyle{ P_n }[/math].

Нормировка по правилу Шмидта

Нормированные по правилу Шмидта полиномы Лежандра выглядят следующим образом:

[math]\displaystyle{ SP^0_n(x) = P^0_n(x), }[/math]

[math]\displaystyle{ SP^m_n(x) = (-1)^m \left(\frac{2(n - m)!}{(n + m)!}\right)^{1/2} P^m_n(x). }[/math]

Сдвинутые многочлены Лежандра

Сдвинутые многочлены Лежандра определяются как [math]\displaystyle{ \tilde{P_n}(x) = P_n(2x - 1) }[/math], где сдвигающая функция [math]\displaystyle{ x\mapsto 2x-1 }[/math] (это аффинное преобразование) выбрана так, чтобы однозначно отображать интервал ортогональности многочленов [math]\displaystyle{ [-1,\; 1] }[/math] на интервал [math]\displaystyle{ [0,\; 1] }[/math], в котором уже ортогональны сдвинутые многочлены [math]\displaystyle{ \tilde{P_n}(x) }[/math]:

[math]\displaystyle{ \int\nolimits_0^1 \tilde{P_m}(x) \tilde{P_n}(x) \,dx = \frac{1}{2n + 1} \delta_{mn}. }[/math]

Явное выражение для смещённых многочленов Лежандра задаётся как

[math]\displaystyle{ \tilde{P_n}(x) = (-1)^n \sum_{k=0}^n \binom{n}{k} \binom{n + k}{k} (-x)^k. }[/math]

Аналогом формулы Родрига для смещенных многочленов Лежандра является

[math]\displaystyle{ \tilde{P_n}(x) = \frac{1}{n!} \frac{d^n}{dx^n} \left[(x^2 - x)^n\right]. }[/math]

Выражения для некоторых первых сдвинутых многочленов Лежандра:

n	[math]\displaystyle{ \tilde{P_n}(x) }[/math]
0	[math]\displaystyle{ 1 }[/math]
1	[math]\displaystyle{ 2x - 1 }[/math]
2	[math]\displaystyle{ 6x^2 - 6x + 1 }[/math]
3	[math]\displaystyle{ 20x^3 - 30x^2 + 12x - 1 }[/math]
4	[math]\displaystyle{ 70x^4 - 140x^3 + 90x^2 - 20x + 1 }[/math]

Матрица функции многочлена Лежандра

[math]\displaystyle{ \begin{pmatrix} 0 & 0 & -2 & 0 & 0 & \vdots & 0 & \vdots & 0 \\ 0 & 2 & 0 & -6 & 0 & \vdots & 0 & \vdots & \vdots \\ 0 & 0 & 6 & 0 & -12 &\vdots & 0 & \vdots & \vdots \\ 0 & 0 & 0 & 12 & 0 & \vdots & 0 & \vdots & \vdots \\ 0 & 0 & 0 & 0 & 20 & \vdots & 0 & \vdots & \vdots \\ \dots & \dots & \dots & \dots & \dots & \ddots & \vdots & \dots & \vdots \\ 0 & 0 & 0 & 0 & 0 &\dots & k(k+1) &\dots & \vdots \\ \dots & \dots & \dots & \dots & \dots &\dots & \dots & \ddots & \vdots \\ 0 & 0 & 0 & 0 & 0 & \dots & 0 & \dots & n(n+1) \\ \end{pmatrix} }[/math]

Эта матрица является верхнетреугольной. Её определитель равен нулю, а собственные значения равны [math]\displaystyle{ k(k + 1) }[/math], где [math]\displaystyle{ k \in \{0,\;1,\;2,\;3,\;\ldots,\;n\} }[/math].

Примеры

Первые 6 многочленов Лежандра

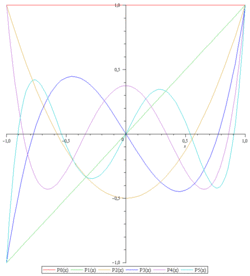
Первые многочлены Лежандра в явном виде:

[math]\displaystyle{ P_0(x) = 1, }[/math]

[math]\displaystyle{ P_1(x) = x, }[/math]

[math]\displaystyle{ P_2(x) = \frac{1}{2} (3x^2 - 1), }[/math]

[math]\displaystyle{ P_3(x) = \frac{1}{2} (5x^3 - 3x), }[/math]

[math]\displaystyle{ P_4(x) = \frac{1}{8} (35x^4 - 30x^2 + 3), }[/math]

[math]\displaystyle{ P_5(x) = \frac{1}{8} (63x^5 - 70x^3 + 15x), }[/math]

[math]\displaystyle{ P_6(x) = \frac{1}{16} (231x^6 - 315x^4 + 105x^2 - 5), }[/math]

[math]\displaystyle{ P_7(x) = \frac{1}{16} (429x^7 - 693x^5 + 315x^3 - 35x), }[/math]

[math]\displaystyle{ P_8(x) = \frac{1}{128} (6435x^8 - 12\,012x^6 + 6930x^4 - 1260x^2 + 35), }[/math]

[math]\displaystyle{ P_9(x) = \frac{1}{128} (12\,155x^9 - 25\,740x^7 + 18\,018x^5 - 4620x^3 + 315x), }[/math]

[math]\displaystyle{ P_{10}(x) = \frac{1}{256} (46\,189x^{10} - 109\,395x^8 + 90\,090x^6 - 30\,030x^4 + 3465x^2 - 63), }[/math]

[math]\displaystyle{ P_{11}(x) = \frac{1}{256} (88\,179x^{11} - 230\,945x^9 + 218\,790x^7 - 90\,090x^5 + 15\,015x^3 - 693x), }[/math]

[math]\displaystyle{ P_{12}(x) = \frac{1}{1024} (676\,039x^{12} - 1\,939\,938x^{10} + 2\,078\,505x^8 - 1\,021\,020x^6 + 225\,225x^4 - 18\,018x^2 + 231), }[/math]

[math]\displaystyle{ P_{13}(x) = \frac{1}{1024} (1\,300\,075x^{13} - 4\,056\,234x^{11} + 4\,849\,845x^9 - 2\,771\,340x^7 + 765\,765x^5 - 90\,090x^3 + 3003x), }[/math]

[math]\displaystyle{ P_{14}(x) = \frac{1}{2048} (5\,014\,575x^{14} - 16\,900\,975x^{12} + 22\,309\,287x^{10} - 14\,549\,535x^8 + 4\,849\,845x^6 - 765\,765x^4 + 45\,045x^2 - 429), }[/math]

[math]\displaystyle{ P_{15}(x) = \frac{1}{2048} (9\,694\,845x^{15} - 35\,102\,025x^{13} + 50\,702\,925x^{11} - 37\,182\,145x^9 + 14\,549\,535x^7 - 2\,909\,907x^5 + 255\,255x^3 - 6435x), }[/math]

[math]\displaystyle{ P_{16}(x) = \frac{1}{32768} (300540195x^{16} - 1163381400x^{14} + 1825305300x^{12} - 1487285800x^{10} + 669278610x^{8} - 162954792x^{6} + 19399380x^{4} - 875160x^{2} + 6435), }[/math]

[math]\displaystyle{ P_{17}(x) = \frac{1}{32768} (583\,401\,555x^{17} - 2\,404\,321\,560x^{15} + 4\,071\,834\,900x^{13} - 3\,650\,610\,600x^{11} + 1\,859\,107\,250x^9 - 535\,422\,888x^7 + 81\,477\,396x^5 - 5\,542\,680x^3 + 109\,395x). }[/math]

Поскольку [math]\displaystyle{ P_n(1) = 1 }[/math], то

[math]\displaystyle{ P_n(x) = \frac{\lambda_0 + \lambda_1 x + \lambda_2 x^2 + \ldots + \lambda_n x^n}{\lambda_0 + \lambda_1 + \ldots + \lambda_n} = \frac{\sum\limits_{i=0}^n \lambda_i x^i}{\sum\limits_{i=0}^n \lambda_i}. }[/math]

Свойства

• Если [math]\displaystyle{ n \neq 0 }[/math], то [math]\displaystyle{ \forall x\in(-1,\;1) \quad |P_n(x)| \lt 1. }[/math]
• Для [math]\displaystyle{ n \neq 0 }[/math] степень [math]\displaystyle{ P_n }[/math] равна [math]\displaystyle{ n }[/math].
• Сумма коэффициентов многочлена Лежандра [math]\displaystyle{ P_n(x) }[/math] равна 1.
• Уравнение [math]\displaystyle{ P_n(x) = 0 }[/math] имеет ровно [math]\displaystyle{ n }[/math] различных корней на отрезке [math]\displaystyle{ [-1,\;1]. }[/math]
• Пусть [math]\displaystyle{ \forall n \in \N \quad U_n(x) = (x^2 - 1)^n }[/math]. Тогда

  [math]\displaystyle{ U'_{n+1}(x) - 2(n + 1)x U_n(x) = 0, }[/math]

  [math]\displaystyle{ (x^2 - 1) U'_n(x) - 2nx U_n(x) = 0. }[/math]

• Присоединённые многочлены Лежандра являются решениями дифференциального уравнения

  [math]\displaystyle{ \frac{d}{dx} \left[(1 - x^2) \frac{d}{dx}P_n(x)\right] - \frac{m^2}{(1 - x^2)} P_n(x) + n(n + 1) P_n(x) = 0. }[/math]

При [math]\displaystyle{ m = 0 }[/math] уравнение принимает вид

[math]\displaystyle{ P'_{n+1}(x) = x P'_n(x) + (n + 1) P_n(x). }[/math]

• Производящая функция для многочленов Лежандра равна

  [math]\displaystyle{ \sum_{n=0}^\infty P_n(z) x^n = \frac{1}{\sqrt{1 - 2xz + x^2}}. }[/math]

• Условие ортогональности этих полиномов на отрезке [math]\displaystyle{ [-1,\;1] }[/math]:

  [math]\displaystyle{ \int\limits_{-1}^1 P_k(x) P_l(x)\,dx = \frac{2}{2k + 1} \delta_{kl}, }[/math]

где [math]\displaystyle{ \delta_{kl} }[/math] — символ Кронекера.

• Для [math]\displaystyle{ n \in \N }[/math] норма [math]\displaystyle{ P_n }[/math] равна

  [math]\displaystyle{ \|P_n\| = \sqrt{\int\limits_{-1}^1 P_n^2(x)\,dx} = \sqrt{\frac{2}{2n + 1}}. }[/math]

• Нормированная функция многочленов Лежандра связана с нормой [math]\displaystyle{ P_n }[/math] следующим соотношением:

  [math]\displaystyle{ \tilde P_n(x) = \frac{P_n(x)}{\|P_n\|} = \sqrt{\frac{2n + 1}{2}} P_n(x). }[/math]

• При каждом [math]\displaystyle{ m \gt 0 }[/math] система присоединённых функций Лежандра [math]\displaystyle{ P^m_n(x),\ n = m,\;m + 1,\;\ldots }[/math] полна в [math]\displaystyle{ L_2(-1,\;1) }[/math].
• В зависимости от [math]\displaystyle{ m }[/math] и [math]\displaystyle{ n }[/math] присоединённые многочлены Лежандра могут быть как чётными, так и нечётными функциями:

  [math]\displaystyle{ P^m_n(-x)=(-1)^{m+n}P^m_n(x). }[/math]

  [math]\displaystyle{ P_{2n} }[/math] — чётная функция,

  [math]\displaystyle{ P_{2n+1} }[/math] — нечётная функция.

• [math]\displaystyle{ P_n(1) = 1. }[/math]
• [math]\displaystyle{ P_n(-1) = (-1)^n. }[/math]
• [math]\displaystyle{ P_{2n}(0) = \frac{1}{2^{2n}} \sum_{k=0}^n(-1)^k \binom{2n}{k} \binom{4n - 2k}{2n} 0^{2n-2k} = \frac{1}{2^{2n}} (-1)^n \binom{2n}{n} }[/math], поскольку [math]\displaystyle{ \forall k \neq n \quad 0^{2n-2k} = 0 }[/math], а [math]\displaystyle{ 0^{2n-2n} = 1 }[/math].
• Для [math]\displaystyle{ n \neq 0 }[/math] выполняется [math]\displaystyle{ P_{2n}(0) \leqslant \frac{1}{\sqrt{\pi n}} }[/math].
• [math]\displaystyle{ \forall x\in[-1,\;1],\;\forall n\in\N^* \quad |P_n(x)|\leqslant \sqrt{\frac{2}{\pi n(1 - x^2)}}. }[/math]

Ряды многочленов Лежандра

См. также: Сумма ряда

Разложение липшицевой функции в ряд многочленов Лежандра

Липшицевая функция [math]\displaystyle{ f }[/math] является функцией со свойством

[math]\displaystyle{ |f(x) - f(y)| \leqslant L|x - y| }[/math], где [math]\displaystyle{ L \gt 0 }[/math].

Эта функция разлагается в ряд многочленов Лежандра.

Пусть [math]\displaystyle{ \varepsilon(I) }[/math] — пространство непрерывных отображений на отрезке [math]\displaystyle{ I = [-1,\;1] }[/math], [math]\displaystyle{ f \in \varepsilon(I) }[/math], и [math]\displaystyle{ n \in \N }[/math].

Пусть

[math]\displaystyle{ c_n(f) = \int\limits_{-1}^1 f(x) \tilde P_n(x)\,dx, }[/math]

тогда [math]\displaystyle{ c_n(f) }[/math] удовлетворяет следующему условию:

[math]\displaystyle{ \lim_{n\to\infty} c_n(f) = 0. }[/math]

Пусть [math]\displaystyle{ S_n f = \sum_{k=0}^n c_k(f) \tilde P_k }[/math] и [math]\displaystyle{ S_nf }[/math] удовлетворяет следующим условиям:

1. [math]\displaystyle{ \forall x \in I \quad S_n f(x) = \int\limits_{-1}^1 K_n(x,\;y) f(y)\,dy }[/math], где [math]\displaystyle{ K_n(x,\;y) = \frac{n + 1}{2} \frac{P_{n+1}(x) P_n(y) - P_{n+1}(y) P_n(x)}{x - y}; }[/math]
2. [math]\displaystyle{ S_n f(x) - f(x) = \int\limits_{-1}^1 K_n(x,\;y) \big(f(y) - f(x)\big)\,dy; }[/math]
3. [math]\displaystyle{ \forall x \in[-1,1] \quad \lim_{n\to\infty} S_n f(x) = f(x). }[/math]

Липшицеву функцию [math]\displaystyle{ f }[/math] можно записать следующим образом:

[math]\displaystyle{ f = \sum_{n=0}^\infty c_n(f) \tilde P_n. }[/math]

Разложение голоморфной функции

Всякая функция [math]\displaystyle{ f }[/math], голоморфная внутри эллипса с фокусами −1 и +1, может быть представлена в виде ряда:

[math]\displaystyle{ f(x) = \sum_{n=0}^\infty \lambda_n P_n(x). }[/math]

Теорема сложения

Для величин, удовлетворяющих условиям [math]\displaystyle{ 0\leqslant \psi_1 \lt \pi }[/math], [math]\displaystyle{ 0\leqslant \psi_2 \lt \pi }[/math], [math]\displaystyle{ \psi_1 + \psi_2 \lt \pi }[/math], [math]\displaystyle{ \varphi }[/math] — действительное число, можно записать теорему сложения для полиномов Лежандра первого рода:

[math]\displaystyle{ P_k (\cos\psi_1\cos\psi_2 + \sin\psi_1\sin\psi_2\cos\varphi) = P_k(\cos\psi_1)P_k(\cos\psi_2) + 2\sum\limits_{m=1}^\infty (-1)^m P_k^{-m}(\cos\psi_1)P_k^m(\cos\psi_2)\cos m\varphi, }[/math]

или, в альтернативной форме через гамма-функцию:

[math]\displaystyle{ P_k (\cos\psi_1\cos\psi_2 + \sin\psi_1\sin\psi_2\cos\varphi) = P_k(\cos\psi_1)P_k(\cos\psi_2) + 2\sum\limits_{m=1}^\infty \frac{\Gamma(k-m+1)}{\Gamma(k+m+1)} P_k^m(\cos\psi_1)P_k^m(\cos\psi_2)\cos m\varphi. }[/math]

Для полиномов Лежандра второго рода теорема сложения выглядит как

[math]\displaystyle{ Q_k (\cos\psi_1\cos\psi_2 + \sin\psi_1\sin\psi_2\cos\varphi) = P_k(\cos\psi_1)Q_k(\cos\psi_2) + 2\sum\limits_{m=1}^\infty (-1)^m P_k^{-m}(\cos\psi_1)Q_k^m(\cos\psi_2)\cos m\varphi }[/math]

при условиях [math]\displaystyle{ 0\leqslant \psi_1 \lt \pi/2 }[/math], [math]\displaystyle{ 0\leqslant \psi_2 \lt \pi }[/math], [math]\displaystyle{ \psi_1 + \psi_2 \lt \pi }[/math], [math]\displaystyle{ \varphi }[/math].

Функции Лежандра

Основная статья: Сферические функции

Многочлены Лежандра (вместе с присоединёнными функциями Лежандра [math]\displaystyle{ P_{n,\;m}(x) }[/math]) естественно возникают в теории потенциала.

Шаровые функции — это функции (в сферических координатах [math]\displaystyle{ r,\;\theta,\;\varphi }[/math]) вида (с точностью до константы)

[math]\displaystyle{ r^n P^m_n(\cos\theta) \cos m\varphi }[/math] и [math]\displaystyle{ r^n P^m_n(\cos\theta) \sin m\varphi, }[/math]

где [math]\displaystyle{ P^m_n }[/math] — присоединённые многочлены Лежандра. Они также представимы в виде [math]\displaystyle{ r^n Y_{nm} }[/math], где [math]\displaystyle{ Y_{nm} }[/math] — сферические функции.

Шаровые функции удовлетворяют уравнению Лапласа всюду в [math]\displaystyle{ \R^3 }[/math].

Литература

• Бейтмен Г., Эрдейи А. Высшие трансцендентные функции = Higher Transcendental Functions / Пер. Н. Я. Виленкина. — Изд. 2-е,. — М.: Наука, 1973. — Т. 1. — 296 с. — 14 000 экз.
• Владимиров В. С., Жаринов В. В. Уравнения математической физики. — М.: Физматлит, 2004. — ISBN 5-9221-0310-5.
• Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений. — Изд. 4-е, перераб. — М.: Государственное издательство физико-математической литературы, 1963. — 19 000 экз.
• Кампе де Ферье Ж., Кемпбелл Р., Петьо Г., Фогель Т. Функции математической физики. — М.: Физматлит, 1963.
• Никольский С. М. Квадратурные формулы. — М.: Наука, 1988.
• Цимринг Ш. Е. Специальные функции и определенные интегралы. Алгоритмы. Программы для микрокалькуляторов: Справочник. — М.: Радио и связь, 1988.

Ссылки

• Legendre Polynomials — University of Rochester, 2010.